1. Waveguide quantum electrodynamics and "giant atoms"
Waveguide quantum electrodynamics (WQED), studying the interaction of quantum emitters with propagating photons, offers novel opportunities both for fundamental physics and for quantum information processing and experiences now a rapid progress driven by novel quantum technologies. The combination of a strong atom-photon interaction with the light-mediated coupling between atoms at large distances makes WQED setups unusual from the point of view of condensed matter physics. For more details see the reviews of WQED: https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.95.015002 and https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.89.021001.
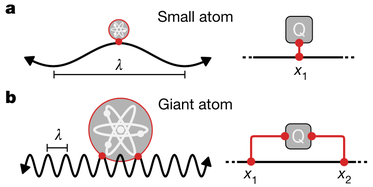
In WQED, single atoms are usually modeled as points [see panel (a) of the figure above]. This tenet nowadays breaks up in so called “giant atoms” (GAs): a GA [see panel (b) of the figure above] is an artificial quantum emitter coupled to the field at many separate points (non-local atom-field interaction). GAs can be implemented in the lab through superconducting qubits coupled to microwave photons or surface acoustic waves. As the distance between different coupling points can be comparable with the field’s wavelength, a GA behaves as a sort of tiny quantum interferometer. As such, it can exhibit unprecedented self-interference effects, which can yield, e.g., a complete decoupling of the atom from the field, making the GA fully “dark”. Even more strikingly and as experimentally confirmed, for suitable coupling points’ arrangements, a set of GAs coupled to a common waveguide can be made fully dissipationless but featuring only a residual coherent photon-mediated interaction. This phenomenon is impossible with normal atoms and realizes a so called (in-band) decoherence-free interaction, a key task in modern quantum technologies for the implementation of large-scale quantum networks. For more details see the short review of giant atoms: https://link.springer.com/chapter/10.1007/978-981-15-5191-8_12 and the dedicated workshop: https://eth-its.ethz.ch/activities/Giant-Atoms.html.
More knowledge: How to simulate a "giant atom" in a synthetic frequency dimension?
The so-called "synthetic frequency dimension" is an artificial dimension constructed from the frequency modes of light, microwaves, or other wave-like excitations. By treating the discrete frequency modes of a system as positions along a synthetic axis, one can create a “lattice” in frequency space. In this synthetic lattice, hopping between frequencies can be engineered using various techniques, such as modulation of resonators or coupling between different frequency modes, mimicking the behavior of particles hopping between sites in a spatial lattice.
When a "giant atom" is realized in a synthetic frequency dimension, it couples to multiple frequency modes simultaneously. This is analogous to how a real-space giant atom interacts with multiple spatial locations but here, the interactions occur in the synthetic lattice of frequency modes. The extended interaction in the synthetic dimension allows the giant atom to couple non-locally within the frequency space, leading to interference effects between different frequency components.
For more details see our paper Phys. Rev. Lett. 128, 223602 (2022).
2. Cavity optomechanics
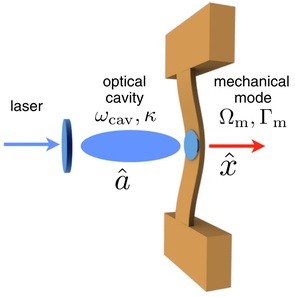
Mechanical resonators, when placed inside an optical cavity, interacts with the light field. This interaction mechanism is based on the principle of radiation pressure forces (see the left figure). Cavity optomechanical devices constitute a leading platform for quantum control of mechanical resonators. Impressive progress has been made in this field by demonstrating, for example, ground state cooling of mechanical motion, single-phonon control, and (opto)mechanical entanglement. Key to enabling this progress has been to increase the coupling rate between light and mechanical motion compared to the energy loss rates in the system. Most experiments in the field, however, operate in a driven regime, which amplifies the optomechanical interaction by use of a coherent laser drive at the expense of loosing its nonlinear character. For more details see the review of cavity optomechanics: https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.86.1391.
In collaboration with Witlef's experimental group and Janine's theoretical group, we aim to achieve a major breakthrough in this field by lifting this limitation such that single quanta of light (photons) and of mechanical motion (phonons) interact nonlinearly and coherently. This breakthrough will allow us to explore novel mechanics-based sensing technologies, in particular, non-destructive detection of single photons via measuring mechanical displacements, and foundational studies targeting the direct generation of optomechanical quantum states.
3. Topological photonics
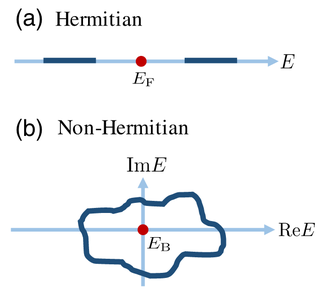
One crucial advantage of topologically protected edge states is that they are robust against fabrication imperfections and disorders. For Hermitian topological insulators (TIs), the bulk-edge correspondence is well explored and understood, and various topological invariants have been proposed to characterize distinct topological phases. However, many realistic physical systems, such as open systems and photonic systems with loss and/or gain, are described by non-Hermitian Hamiltonians, the topological properties of which are intensively being investigated. Topological photonics, in particular, has attracted a great deal of interest accompanied with rapid progress. The experimental realization of topological edge states in a lossy waveguide array has revived the debate about the bulk-edge correspondence for non-Hermitian TIs, a notion that is reconsidered in systems exhibiting an anomalous localization or non-Hermitian skin effect, whereas in other instances it holds true as typically described by topological invariants. Compared with condensed-matter electronic systems, photonic systems exhibit three major advantages in studying topological effects:
(i) in photonics, loss and gain are ubiquitous and can be controlled;
(ii) optical nonlinearities enable richer phenomena in topological photonics;
(iii) due to various internal degrees of freedom, it is possible to realize synthetic dimensions in photonic systems.
To date, a lot of breakthroughs have been achieved based on such properties, such as optical delay lines with enhanced transport properties, backscattering-free edge states, topological lasers and sensors, and topological polaritons, to name a few. For more details see the reviews of topological photonics: https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.91.015006 and https://journals.aps.org/prx/abstract/10.1103/PhysRevX.8.031079.
Lei is now involved in the project
He also regularly collaborates with many outstanding researchers, including:
Anton Frisk Kockum (Chalmers University of Technology)
Lingzhen Guo (Tianjin University)
Yong Li (Hainan University)
Jin-Hui Wu (Northeast Normal University)
Giuseppe La Rocca (Scuola Normale Superiore di Pisa)
Maurizio Artoni (European Laboratory for Non-Linear Spectroscopy)
Juliette Monsel (Chalmers University of Technology)
Zhihai Wang (Northeast Normal University)
Xin Wang (Xi'an Jiaotong University)